No One Does Math(s) These Days
When I was a kid I wanted to grow up and become a doctor. You may already know this, but I am not a doctor. Why? Well, it turns out that in order to practice medicine, you have to be able to do math. Math and I, historically, have not gotten along.
In grade school, I struggled through my multiplication tables and fought tooth and nail for a hard-won understanding of fractions. But that knowledge has receded over time.
Thanks to my handy pocket calculator (iPhone), I was able to get through life without so much as having to calculate 20% of a restaurant check in my head. For many adult humans (including Peep Show's Jeremy), math has gone the way of the dodo. We don't need to understand it, so whatever basic knowledge we crammed into our brains during grade school has just been forgotten.
Given my earlier struggles with even the most basic of mathematical concepts, imagine my surprise when I found myself learning how to program and loving it. Through high school and college I developed an idea of myself as someone who was profoundly un-technical. The fact that I couldn't do math became part of my identity. I was the type of person who saw my computer as magical metal movie-watching box, and I was fine with that.
Later, after I found my way to programming, I began to shed my "non-technical" identity and trust in my capability to learn and master technical concepts and skills.
Fast forward a few years and I'm a fairly proficient programmer (if you don't mind my saying so), but I've come to realize that I never really questioned my "I can't do math" identity. Instead, I've been carrying non-technical Sophie around with me all of this time.
Yesterday she reared her head again during an otherwise innocuous attempt to change the permissions on a file on my computer. Many of us late-comers to programming, who share an aversion to or lack of experience with math, have memorized the basic set of file permissions.
Oh sure, we know that chmod 777 gives read, write, execute permissions to everyone, and chmod 600 gives read write permissions to our own user. But I for one, have never understood how these magical numbers were calculated, or what they meant.
But now, thanks to a co-worker's simple question of "Do you know how we get to 777?", my answer of "F**k no", and a subsequent eye-opening tutorial, I do totally understand it, and the basics of the binary system to boot. Keep reading and pretty soon you will to!
The Base-10 System
Before we can understand binary, or the Base-2 system, we need to understand our own every-day Base-10 system. So, what is it?
Our everyday number system is a Base-10 system.
The Base-10 number system is known as the decimal system and has 10 digits to show all numbers
0,1,2,3,4,5,6,7,8,9
Appropriately, this quote is taken from http://www.amathsdictionaryforkids.com/.
So, how does the Base-10 system work? Let's start by mapping out a number to a set of indexed columns.
Let's use the number 2,348
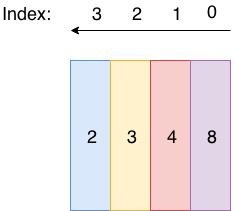
With the following steps, we will understand how the collection of digits––2, 3, 4, 8––actually indicate the number two thousand three hundred and forty-eight.
Notice that each digit lives in a column that is mapped to an index number. The 8 is at index 0, the 4 at index 1, and so on.
Here is where our base number comes in.
Our base number is 10 (Base-10 system, remember). For each column, we want to multiply the number that lives in the column by the base number to the power of the index that we are on. Let's map the index positions, or columns, to the appropriate Base-10 value.
- Index 0:
10^0 = 1* - Index 1:
10^1 = 10, i.e.10 x 1 - Index 2:
10^2 = 100, i.e.10 x 10 - Index 3:
10^3 = 1000, i.e.10 x 10 x 10
For each index position, we raise our base value to the power of the index position.
*Note: any number to the 0 power equals (drum roll please....) 1! I literally did not know this until yesterday. If you also did not know this––you are not alone!
Now, our column map looks something like this:
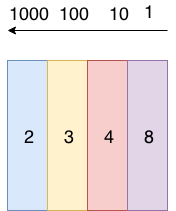
The last step is to multiply each of the values contained in the columns by its corresponding Base-10 value.
8 x 1 = 84 x 10 = 403 x 100 = 3002 x 1000 = 2000
Then, we add up these products
8 + 40 + 300 + 2000 = 2,348
We did it!
Honestly what does it tell you that all of the resources I am using for this post are aimed at children?
Now that we understand how the Base-10 system works, let's take a look at Binary, or the Base-2 system.
Binary, the Base-2 system
The Binary system works exactly like the Base-10 system. Instead of using 10 digits, the numbers 0-9, to represent all numeric values, we use two digits, 0-1.
In the previous section, we looked at the sequence of numbers 2, 3, 4, 8 and came to understand that, using a Base-10 system, they represented the value of two thousand three hundred and forty-eight.
Let's do a similar exercise with the Base-2 system.
We'll come to understand how the Binary number 100100101100 represents the same value of two thousand three hundred and forty-eight.

Here, we've once again mapped the index value to the Base value by raising the base value to the power of the index number:
- Index
0:2 ^ 0 = 1 - Index
1:2 ^ 1 = 2 - Index
2:2 ^ 2 = 4 - Index
3:2 ^ 3 = 8 - Index
4:2 ^ 4 = 16 - Index
5:2 ^ 5 = 32 - Index
6:2 ^ 6 = 64 - Index
0:2 ^ 7 = 128 - Index
0:2 ^ 8 = 256 - Index
0:2 ^ 9 = 512 - Index
0:2 ^ 10 = 1024 - Index
0:2 ^ 11 = 2048
Then, we take the binary value present at each index number and multiply it by the results from above.
- Index
0:1 x 0 = 0 - Index
1:2 x 0 = 0 - Index
2:4 x 1 = 4 - Index
3:8 x 1 = 8 - Index
4:16 x 0 = 0 - Index
5:32 x 1 = 32 - Index
6:64 x 0 = 0 - Index
0:128 x 0 = 0 - Index
0:256 x 1 = 256 - Index
0:512 x 0 = 0 - Index
0:1024 x0 = 0 - Index
0:2048 x 1 = 2048
The last step is to calculate the sum of the above products:
0 + 0 + 4 + 8 + 0 + 32 + 0 + 0 + 256 + 0 + 0 + 2048 = 2,348
We did it! If this approach seems formulaic––you're right! I bet it would lend itself really well to abstraction. It might be fun to write a Ruby method (or whatever language you prefer) to calculate the numeric value of a given Binary number...just sayin'.
Now that we've mastered Binary (we're so smart), let's take a look at applying it to file permissions calculations we discussed earlier.
Binary and File Permissions
Let's take the example of setting a permission of 777 on a given file. Each digit here represents a different entity to whom you are granting the permission:
you | group | all
We know (and soon we'll understand why), that a permission of 7 means you are granting the entity read-write-execute access (all the access!)
Where does the number 7 come from? Why does that translate to read-write-execute access?
Let's break it down with Binary.
The permission of 7 is actually composed of binary digits, each of which maps to a read, write and execute permission respectively.

The execute permission is mapped to index 0, the write permission is mapped to index 1 and the read permission is mapped to index 2.
The Binary values for each of these index positions, or columns, indicates whether or not we are granting this permission. We set a value of 1 for "yes" and 0 for "no". This gives us the binary number: 111.
Then, we use our Base-2 calculation system to get the numeric value of this binary number.
For each index position, we multiply the binary value by the Base-2 value. The Base-2 value is calculated by raising the base value, 2, to the power of the index number.
Base-2 value calculations:
- Index
0:2 ^ 0 = 1 - Index
1:2 ^ 1 = 2 - Index
2:2 ^ 2 = 4
Product calculations: binary value x base-2 value
- Index
0:1 x 1 = 1 - Index
1:1 x 2 = 2 - Index
2:1 x 4 = 4
Lastly, we calculate the sum:
1 + 2 + 4 = 7
7 is therefore the numeric representation of 111, which is the binary representation of "yes you can read", "yes you can write", "yes you can execute" this file. That one digit, 7, nicely encodes three separate pieces of information regarding the entity's permissions to read, write and/or execute the file. All of a sudden, that number seems a whole lot less mysterious.
Conclusion
This has been an extremely basic introduction to the concept of Binary, with a brief look at understanding the role it plays in the everyday action of changing file permissions. Hopefully, this article serves to demystify some concepts that can seem out of reach for former Luddites like myself. I hope you'll dive deeper––I know I plan to.
Happy coding!


